Decibel Tutorial: dB og dBm vs. Gain and Milliwatts

Konseptet med en desibel (dB) er forståelig vanskelig og forvirrende for noen som bare blir introdusert for det. Å kombinere spesifikasjoner for forsterkning, kraft og spenning (og strøm, men ikke så ofte) som blander dB, dBm, dBW, watt, milliwatt, spenning, millivolt osv., Krever ofte konvertering frem og tilbake mellom lineære verdier og desibelverdier. Denne korte opplæringen vil bidra til å tydeliggjøre forskjellen mellom å jobbe med desibel og å jobbe med lineære verdier.

Logaritmer (logger) ble først unnfanget i de tidlige 1600-ene av den skotske matematikeren John Napier, som et verktøy for å forenkle multiplikasjons- og divisjonsoperasjoner ved å konvertere dem til henholdsvis raskere og mindre feilutsatte tilleggs- og subtraksjonsoperasjoner. Dette er muliggjort på grunn av måten multiplikasjon av to tall uttrykt som lignende basistall med eksponenter kan oppnås ved bare å legge eksponentene sammen. Delingen av de samme tallene oppnås ved å trekke eksponentene fra. Det er en av lovene til eksponenter, og ser slik ut:

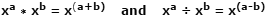
Bruke faktiske tall som eksempel, der x = 10, a = 4, b = 1:

Loven til eksponenter fungerer for et hvilket som helst basenummer, ikke bare 10. For å vite:

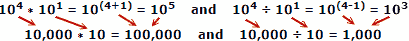
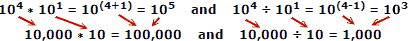
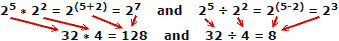
Folk har en tendens til å gjøre færre feil når de legger til og trekker fra tall, så fordelen med logaritmer er åpenbar. Husk at logaritmer ble utviklet før automatiske mekaniske eller elektroniske datamaskiner var tilgjengelige. En lysbilde-regel utnytter egenskapene til logaritmer for beregning, men det er et eget hovedtema.

Dette er enkle eksempler, men gjelder for enhver base eller eksponent. I mangel av kalkulator, trenger du en tabell med tall og tilsvarende logaritmer for å være nyttig for generell bruk. Tidlige loggtabeller fylte volum, avhengig av avstand mellom tall (1.000, 1.001, 1.002, 1.003, vs. 1.0, 1.1, 1.2, 1.3, etc.). Den gode nyheten for skapere av logaritmetabeller er at bare et enkelt 'tiår' med tall (f.eks. 1 til 10) er nødvendig, siden hvert foregående eller avskjedende tiår er en enkel multiplum av en styrke på 10.

Merk: Jeg bruker base 10 i denne diskusjonen siden det er basen i vårt vanlige tallsystem - derav begrepet 'felles logaritme' for base 10 logger. Du har kanskje hørt om naturlige logaritmer, som bruker basen til e, men e brukes ikke så ofte når du beregner skalær elektrisk kraft, spenning og strømmengder (selv om den brukes når fasevinkler er inkludert, dvs. Eulers identitet). Naturlige logaritmer er skrevet som ln (x) uten 'e' -underskriptet, mens vanligvis base 10-logaritmer skrives ganske enkelt som logg (x) uten 10-abonnementet; dvs. ikke henholdsvis loge (x) eller log10 (x).

Per en base = 10 loggbord:

Semi-logaritmisk 5 Cycles Engineering Grafikkpapir - RF Cafe Unntaket og spesielle tilfeller er logx (0) = udefinert. Det er slik fordi det ikke er noen kraft du kan heve et hvilket som helst tall og få 0 (null). Du kan asymptotisk nærme deg null, men du kan ikke komme til null. Det vil aldri bli tallet null som vises på en loggskala; de løper vanligvis fra en viss kraft av 10 til en annen kraft på ti. Et eksempel på loggpapir vises til høyre. Den har 5 'sykluser' eller 'tiår' av rekkevidde. Merk at det ikke er null på y-aksen.

Basen-10 (vanlig) logaritme for et tall er da eksponenten som 10 må heves til for å få dette tallet. Med andre ord, siden 10 hevet til kraften til 2 er lik 100 (102 = 100), er basen-10-loggen til 100 2 (log10 100 = 2).

Dette er den grunnleggende loven om logaritmer:


Utføre de samme multiplikasjonene og divisjonene som gjort øverst på siden ved å bruke faktiske logaritmer:



Det er greit, men det du ender opp med er logaritmen til antallet du søker. Spørsmål: Bortsett fra et enkelt eksempel som dette, hvordan får du svaret du trenger? Svar: Slå opp antilogaritmen (antilog) for resultatet. I dette tilfellet:

Et tøffere og mer sannsynlig eksempel med tall som ikke er heltalskrefter av 10, kan se ut som følgende:




 HP-35-kalkulator (wikipedia) - RF CafeSå logaritmen til 'x' tilsvarer 1.8444, antilog tilsvarer 'x', som er 69.9



Jeg brukte kalkulatoren min til å slå opp loggene og verktøyene for disse tallene, men før 1972 da Hewlett Packard (HP) introduserte sin vitenskapelige HP-35-kalkulator, var den gjennomsnittlige personen uten tilgang til en hoved- eller universitetsdatamaskin for å bruke en logg tabell for å utføre slike beregninger.

Hvem plager å bruke logaritmer i dag, kan du spørre? Mange mennesker, inkludert meg, ganske ofte når jeg beregner kaskaderte systemparametere som støyfigur (NF) og avlyttingspunkter (IP). Enkel tillegg og subtraksjon av dBm- og effekt-dBm-verdier fungerer ikke med NF og IP. De styrende formlene bruker multiplikasjon og inndeling av lineære forsterknings- og effektverdier, som først krever konvertering av dB og / eller dBm til lineære tall (forsterkningsforhold og mW) ved å bruke antilogs, utføre kaskadeberegningene og deretter konvertere resultatet tilbake til dB og / eller dBm ved å bruke logger.

Ikke alle systemkaskadeoperasjoner krever konvertering frem og tilbake. For eksempel hvis bare det er nødvendig med den totale systemforsterkningen og / eller utgangseffektnivået, kan beregninger utføres med enten lineære enheter (mW og multiplikatorer) eller logaritmiske enheter (henholdsvis dBm og dB).

Definisjonen av 'dB' og 'dBm'

En desibel (dB) i elektroteknikk er definert som 10 ganger base-10-logaritmen med et forhold mellom to effektnivåer; f.eks Pout / Pin (gain, med andre ord). For å vite:

Alle gevinster større enn 1 blir derfor uttrykt som positive desibel (> 0), og gevinster på mindre enn 1 uttrykkes som negative desibel (<0). Merk at i tilfeller de fleste av oss møter, må det lineære forholdet mellom P1 / P2 være et positivt tall (> 0) siden logaritmen til 0 er udefinert og logaritmen til negativtall er kompleks (de inneholder både en reell og en imaginær del ). DB-verdien kan imidlertid teoretisk ta en hvilken som helst verdi mellom −∞ og + ∞, inkludert 0, som er en forsterkning på 1 [10 * log (1) = 0 dB].

'dBm' er en desibel-basert kraftenhet som er referert til 1 mW. Siden 0 dB forsterkning er lik en forsterkning på 1, er 1 mW effekt 0 dB større enn 1 mW, eller 0 dBm. Tilsvarende er en kraftenhet på dBW desibel i forhold til 1 W effekt.


Følgelig er alle dBm-verdier større enn 0 større enn 1 mW, og alle dBm-verdier mindre enn 0 er mindre enn 1 mW (se fig. 1). For eksempel er + 3.01 dBm 3.01 dB større enn 1 mW; dvs. eller 0 dBm + 3.01 dB = + 3.01 dBm (2 mW). −3.01 dBm er 3.01 dB mindre enn 1 mW; dvs. eller 0 dBm + (−3.01) dB = −3.01 dBm (0.5 mW).

Tabellen nedenfor gir noen numeriske eksempler slik at du kan se sammenhengen mellom mW og dBm. Det samme settet med verdier plottet i en logaritmisk skala ville gi en rett linje. På grunn av det logaritmiske forholdet, grupperer grafen de mindre verdiene mot den venstre vertikale aksen. En forstørret versjon av 0 til 1 mW-regionen er satt inn for klarhet.

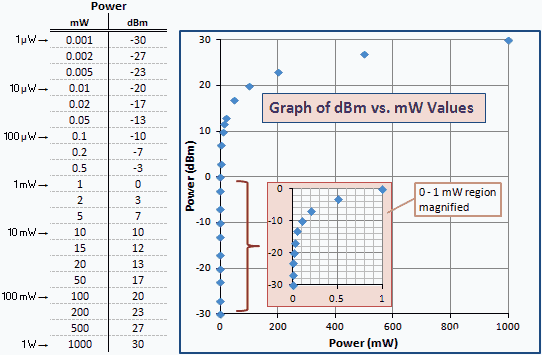
Fig. 1 - Graf over kraft i enheter av dBm vs. mW

Fig. 2 er en tabell og graf over dB vs. lineære forsterkningsforhold som ligner på dBm vs. mW i fig. 1. Merk at tallene og kurvene er nøyaktig de samme. bare aksetikettene blir endret. Det er fordi dBm er en kraftenhet uttrykt i dB i forhold til 1 mW (0 dBm).

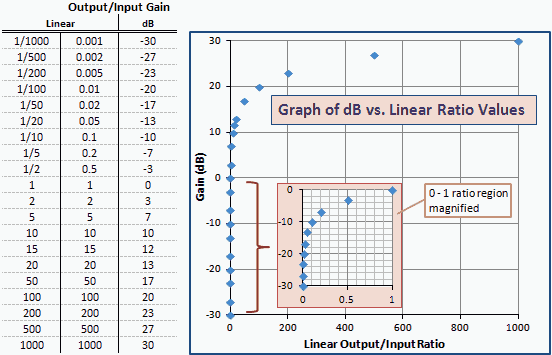
Fig. 2 - Graf over gevinst i enheter av dBm vs. lineær forhold

Fundamentalt er gevinst en multiplikasjons- (eller divisjons) faktor. Som et eksempel kan en forsterker ha en forsterkning som øker signalet med en faktor 4 (dvs. 4x) fra inngang til utgang (se fig. 3). Hvis et 1 mW (0 dBm) signal mates inn i forsterkeren, kommer 1 mW * 4 = 4 mW ut. Når det gjelder desibel, tilsvarer en faktor 4 10 * log (4) = 6.02 dB, så 0 dBm i pluss 6.02 dB gevinstutbytte + 6.02 dBm ved utgangen.

1 mW * 4 = 4 mW

0 dBm + 6.02 dB = 6.02 dBm

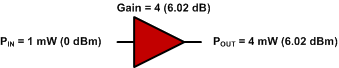
Fig. 3 - Forsterkning av enkeltforsterker.

Kombinere gevinster (lineær og dB) m / positiv verdi

Hvis en forsterker med en forsterkning på 4 er i serie med en andre forsterker med en forsterkning på 6, er den totale forsterkningen 4 * 6 = 24. Når det gjelder desibel, er en faktor på 6 ekvivalent med 10 * log (6) = 7.78 dB, og en faktor på 24 tilsvarer 10 * log (24) = 13.8 dB.

Akkurat som 4 x 6 = 24 (lineær forsterkning), 6.02 dB + 7.78 dB = 13.8 dB (desibel gain).

Hvis et 1 mW-signal (0 dBm) mates inn i forsterkeren, kommer 4 mW ut av den første forsterkeren, og 24 mW kommer ut av den andre forsterkeren. Se fig. 4.

1 mW * 4 * 6 = 24 mW
0 dBm + 6.02 dB + 7.78 dB = 13.8 dBm

Fig. 4 - Forsterket dobbel forsterkningsforsterkning.

Kombinere gevinst og tap (lineær og dB)
Dette neste eksemplet viser hva som skjer når det oppstår en forsterkning <1 (et tap), der en demper med en forsterkning på 1/6 plasseres etter den første forsterkeren i stedet for å ha en andre forsterker. Se fig. 5.
4 * 1 / 6 = 2 / 3 (lineær forsterkning). Tilsvarende 6.02 dB - 7.78 dB = −1.76 dB (desibel gain).
Som med forrige eksempel, hvis et 1 mW signal (0 dBm) mates inn i forsterkeren med en forsterkning på 4, så kommer 4 mW ut. Den 4 mW går så inn i demperen med en lineær forsterkning på 1 / 6 og kommer ut på et effektnivå på 4 / 6 mW (2 / 3 mW).
Den totale gevinsten i dette tilfellet er 4 / 6 = 2 / 3, så utgangseffekten vil faktisk være mindre enn inngangseffekten.

1 mW * 4 * 1 / 6 = 2 / 3 mW = 0.67 mW

0 dBm + 6.02 dB + (-7.78 dB) = −1.76 dBm

Fig. 5 - Forsterket forsterkningsforsterkning og demper.

12 mW + 34 mW + 8 mW + 20 dB

Tilleggsinformasjon om logaritmer
Logaritmer om produkter
En egenskap med logaritmer som brukes implisitt ovenfor, sier følgende, og er grunnlaget for å kunne legge til og trekke fra logaritmerverdier i stedet for å multiplisere deres lineære ekvivalenter.

'h * j / k * m / n' kan representere en kaskade av komponenter som har tre enheter (h, j og m) hver med forsterkning> 1 og to enheter (k og n) hver med forsterkning <1 (se Fig. 6). Den totale systemforsterkningen kan beregnes ved å multiplisere alle de lineære forsterkningsverdiene sammen eller legge alle desibelforsterkningsverdiene sammen.

Fig. 6 - Kaskaderede komponenter

Logaritmer av eksponenter
Følgende er viktig for å forstå hvorfor effektforsterkning i form av kraft er 10 * log (Pout / Pin) dB, mens effektøkning når det gjelder spenning er 20 * log (Vout / Vin) dB.


som er slik fordi cf er lik c ganget med seg selv 'f' ganger. For eksempel, hvis f = 4:


Power Gain Basert på Power vs. Power Gain Basert på Voltage
Power gain er Pout / Pin, og spenningsforsterkning er Vout / Vin. Effektforsterkning basert på et effektforhold i desibel er definert som 10 * log (Pout / Pin). Effektgevinst når det gjelder spenning, er [(Vout2 / R) / (Vin2 / R)], siden per Ohms lov P = V2 / R. 'R' i nevnerne avbryter å forlate Vout2 / Vin2, som er lik (Vout / Vin) 2, som definert av regelen for eksponenter som sier at ac / bc = (a / b) c. Derfor:

Viktig merknad: Spenningsforsterkning når det gjelder spenning er 10 * log (Vout / Vin) dB, det samme som med effektforsterkning når det gjelder effekt. Det er først når effektforsterkning uttrykkes i form av spenning at 20 * loggen (Vout / Vin) dB-ligningen gjelder. Dette er et vanlig forvirringspunkt.


Ingen operasjoner i matematikk er vilkårlig, og det er grunnen til at et signaleffekttap (forsterkning <1) blir fremstilt som en negativ verdi, og derfor blir trukket under en kaskadeberegning. Det er en enkel demonstrasjon, men verdig å nevne.

logg (1 / f) = logg (1) - logg (f) = 0 - log (f) = -log (f)

Hvis du ønsker å bygge en radiostasjon, kan du øke FM-radiosenderen eller trenger andre FM-utstyr, Ta gjerne kontakt med oss: [e-postbeskyttet].

Legg igjen en beskjed 

Meldingsliste